2-D Shapes (Chapters 1 & 2)
Lesson 5: Optimizing Rectangles (2.5)
Learning Goals of Lesson 5
By the end of this lesson, I can:
-explain why a rectangle whose length is twice its width maximizes area with a given perimeter for 3 sides only
-find the dimensions of the rectangle that provide the
maximum area when the given perimeter is for 3 sides only
-solve maximum and minimum measure problems of rectangles
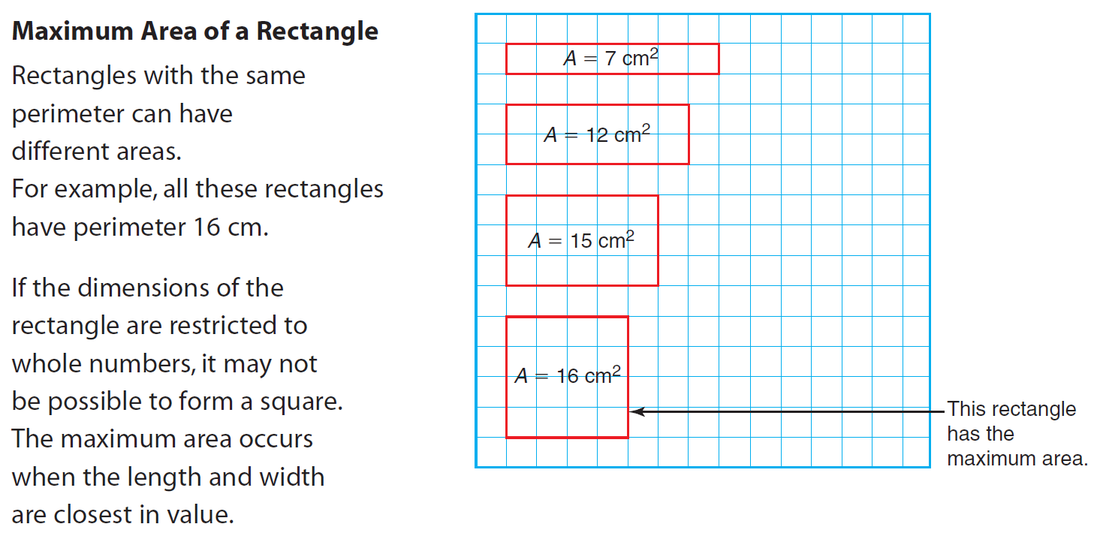
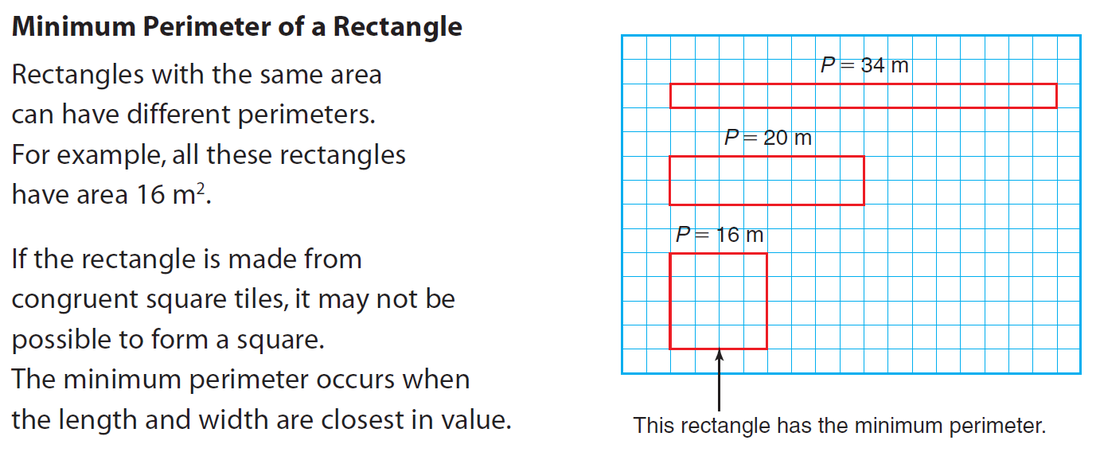
Recall: The Optimal Rectangle is a Square!
It's true when we have a fixed perimeter!
It's also true when we have a fixed area!
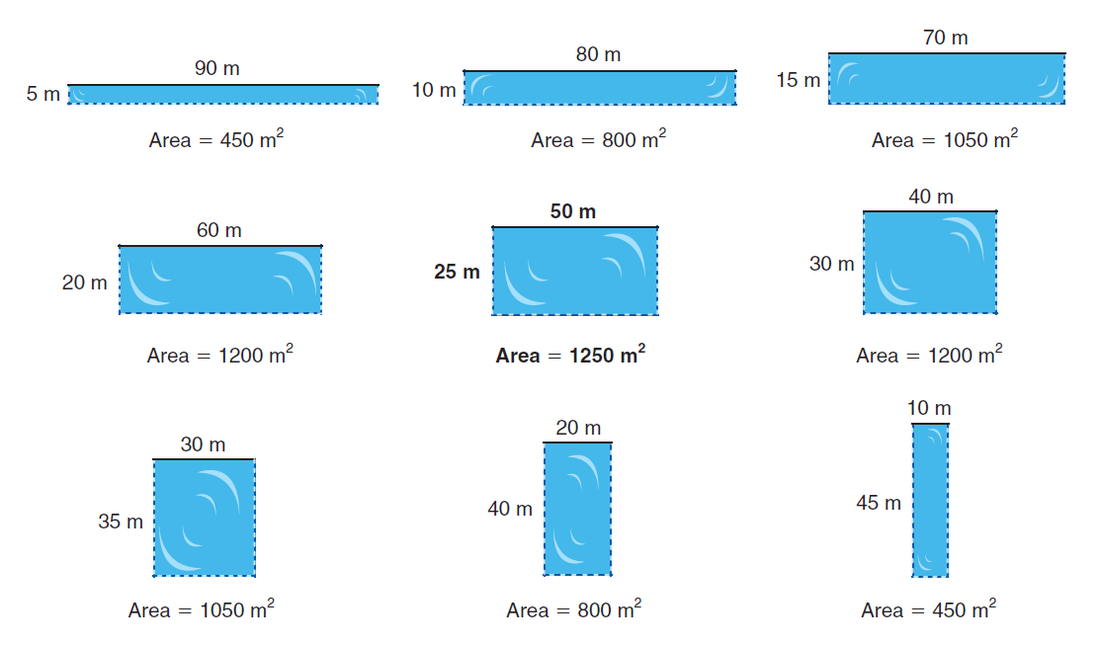
But it's NOT true in the following situation!!
The rope or perimeter given is for 3 sides not 4 sides.
Check out the various possible dimensions of the rectangular
swimming area that can be enclosed by 100 m.
Does a square give you the maximum area?
What dimensions give you the maximum area?
Is there a special relationship between the length and width?
Check out the various possible dimensions of the rectangular
swimming area that can be enclosed by 100 m.
Does a square give you the maximum area?
What dimensions give you the maximum area?
Is there a special relationship between the length and width?
Video 1: Optimizing Area/Perimeter with 3 Enclosed Sides
|
Worksheet 1-8:
|
| ||||||
Smartboard Class Notes
| september_13.pdf | |
| File Size: | 312 kb |
| File Type: | |